HORA DE PROGREDIR NOS ESTUDOS.
HORA DE PROGRESSÃO GEOMÉTRICA DO TIPO QUE OCORRE EM NOSSO PAÍS E FAZ BEM PARA A PREVIDÊNCIA....SEI NÃO....
Olha esses números:
(2, 10, 50, 250, ...)
De novo!
(2, 10, 50, 250, ...)
Viu que estão colocados em ordem crescente?
Sim,mas aqui,existem outros critérios para determinar uma PG em acordo com sua razão, em crescente ou decrescente.
ótimo.
Conhece uma operação matemática que não precisa de anestesista chamada divisão?
Aquela que divide...coisa e tal....então, vamos começar,
O Raciocínio lógico ensina as criancinhas que mesmo sem muitas informações se retira de onde se tem mais e divide com onde tem menos, discordo deste ensino, mas é assim que ensinam.
Nesta sequência, a partir do 2 número que é 10, vamos montar divisões, o sucessor com anterior, assim:
10: 2 5:10 250:50
Então, na divisão,o resultado é denominado QUOCIENTE da divisão.
Se montarmos essas divisões, teremos:
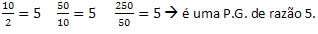
O número 5 é o resultado de todas as divisões, não é mesmo?
Ele é o QUOCIENTE das divisões e a RAZÃO da PG
PG é um "negócio" da matemática que aparece em concursos a nível médio de instrução escolar.
Se define pela "constância do quociente",ou seja, mesmo quociente para todas as divisões se TORNANDO A RAZÃO DA PG.
Entenderam tudinho?
Veja alguns exemplos de sequências numéricas que são progressões geométricas:
(2, 6, 18, 54, 162, 486, 1458, 4374,...) razão q = 3, pois 6:2 = 3
(-5, 15, -45, 135, -405, 1215, ...) razão q = -3, pois 135:(-45) = -3
(3, 15, 75, 375, 1875, 9375,...) razão q = 5, pois 9375:1875 = 5
Uma P.G. pode ser classificada de acordo com a sua razão (q).
Alternada ou oscilante: quando q < 0.
Crescente: quando [a1 > 0 e q > 1] ou [a1 < 0 e 0 < q < 1].
Decrescente: quando [a1 > 0 e 0 < q < 1] ou [a1 < 0 e q >1]
Termo Geral de uma P.G.
Conhecendo o primeiro termo (a1) e a razão (q) de uma progressão geométrica determinamos qualquer termo, basta utilizarmos a seguinte expressão matemática:
an = a1*qn – 1
Exemplos
a5 = a1 * q4
a12 = a1 * q11
a15 = a1 * q14
a32 = a1 * q31
a100 = a1 * q99
Exemplo 1
Determine o 9º termo da P.G. (2, 8, 32,...).
a1 = 2
q = 8:2 = 4
an = a1 * qn-1
a9 = a1 * q9-1
a9 = 2 * 48
a9 = 2 * 65536
a9 = 131072
Exemplo 2
Dada a P.G. (3, -9, 27, -81, 243, -729, ...), calcule o 14º termo.
a1 = 3
q = -9:3 = -3
an = a1 * qn-1
a14 = 3 * (-3)14-1
a14 = 3 * (-3)13
a14 = 3 *(-1.594.323)
a14 = - 4.782.969 (resultado negativo devido ao jogo de sinais ( + ) x ( - ) = - )
Exemplo 3
Calcule o 8º termo da P.G. (-2, -10, -50, -250, ...).
a1 = -2
q = (-10):(-2) = 5
an = a1 * qn-1
a8 = -2 * q8-1
a8 = -2 * 57
a8 = -2 * 78.125
a8 = - 156.250
(resultado é negativo porque assim o é no jogo de sinais (-) x (+) = - ),persistindo dúvidas, consultem:
http://escolakids.uol.com.br/multiplicacao-e-divisao-de-numeros-negativos.htm
As progressões possuem diversas aplicações, um bom exemplo são as estações do ano que se repetem obedecendo a um determinado padrão. No Egito antigo os povos se baseavam em estudos sobre progressões no intuito de saberem os períodos de enchente do rio Nilo, para organizarem suas plantações.
As progressões geométricas são sequências numéricas que apresentam uma característica em comum: cada elemento, a partir do segundo, é obtido realizando o produto entre o termo anterior e uma constante q, denominada de razão da PG. Podemos notar a utilização das progressões em diversas áreas do conhecimento. Os pitagóricos já haviam descoberto, por exemplo, que na escala musical, os valores das frequências das sequências de notas de uma oitava, formam uma progressão geométrica.
Dentre os tópicos abordados no estudo da PG, temos a interpolação de meios geométricos. Interpolar meios geométricos entre dois números dados, a1 e an, é acrescentar números entre os dois que já foram dados para que a sequência numérica formada seja uma PG. Para realizar a interpolação de meios geométricos basta conhecer o valor da razão da progressão geométrica e utilizar a fórmula do termo geral:
an = a1?q(n-1)
Onde,
a1 → é o primeiro termo da PG.
an → é o último termo da PG.
n → é o número dos termos da PG.
Vejamos alguns exemplos para melhor compreensão:
Exemplo 1. Interpole cinco meios geométricos entre 7 e 5103.
Solução: Interpolar cinco meios geométricos entre 7 e 5103 equivale a dizer que devemos acrescentar cinco números entre 7 e 5103 para que a sequência formada seja uma PG.
(7, _, _, _, _, _, 5103)
Para isso, devemos encontrar o valor da razão dessa PG. Pela análise do exercício, temos que:
a1 = 7 e a7 = 5103 e n = 7 (pois a sequência apresenta 7 termos).
Utilizando a fórmula do termo geral, obtemos:
Dentre os tópicos abordados no estudo da PG, temos a interpolação de meios geométricos. Interpolar meios geométricos entre dois números dados, a1 e an, é acrescentar números entre os dois que já foram dados para que a sequência numérica formada seja uma PG. Para realizar a interpolação de meios geométricos basta conhecer o valor da razão da progressão geométrica e utilizar a fórmula do termo geral:
an = a1?q(n-1)
Onde,
a1 → é o primeiro termo da PG.
an → é o último termo da PG.
n → é o número dos termos da PG.
Vejamos alguns exemplos para melhor compreensão:
Exemplo 1. Interpole cinco meios geométricos entre 7 e 5103.
Solução: Interpolar cinco meios geométricos entre 7 e 5103 equivale a dizer que devemos acrescentar cinco números entre 7 e 5103 para que a sequência formada seja uma PG.
(7, _, _, _, _, _, 5103)
Para isso, devemos encontrar o valor da razão dessa PG. Pela análise do exercício, temos que:
a1 = 7 e a7 = 5103 e n = 7 (pois a sequência apresenta 7 termos).
Utilizando a fórmula do termo geral, obtemos:
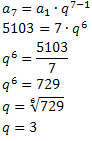
Conhecendo o valor da razão da PG podemos determinar os cinco termos que devem ficar compreendidos entre 7 e 5103.
a2 = a1*q = 7*3 = 21
a3 = a2*q = 21*3 = 63
a4 = a3*q = 63*3 = 189
a5 = a4*q = 189*3 = 567
a6 = a5*q = 567*3 = 1701
Portanto, interpolando cinco meios geométricos entre 7 e 5103, obtemos a PG:
(7, 21, 63, 189, 567, 1701, 5103)
Exemplo 2. Distribua 4 números entre 800 e 25 para que a sequência numérica formada seja uma progressão geométrica.
Solução: Queremos interpolar 4 meios geométricos entre 800 e 25.
(800, _, _, _, _, 25)
Precisamos conhecer o valor da razão dessa PG. Para isso, utilizaremos a fórmula do termo geral.
Sabemos que: n = 6, a1 = 800 e a6 = 25. Segue que:
a2 = a1*q = 7*3 = 21
a3 = a2*q = 21*3 = 63
a4 = a3*q = 63*3 = 189
a5 = a4*q = 189*3 = 567
a6 = a5*q = 567*3 = 1701
Portanto, interpolando cinco meios geométricos entre 7 e 5103, obtemos a PG:
(7, 21, 63, 189, 567, 1701, 5103)
Exemplo 2. Distribua 4 números entre 800 e 25 para que a sequência numérica formada seja uma progressão geométrica.
Solução: Queremos interpolar 4 meios geométricos entre 800 e 25.
(800, _, _, _, _, 25)
Precisamos conhecer o valor da razão dessa PG. Para isso, utilizaremos a fórmula do termo geral.
Sabemos que: n = 6, a1 = 800 e a6 = 25. Segue que:
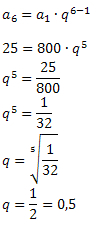
Conhecido o valor da razão, podemos determinar os termos que devem ficar compreendidos entre 800 e 25.
a2 = a1*q = 800*0,5 = 400
a3 = a2*q = 400*0,5 = 200
a4 = a3*q = 200*0,5 = 100
a5 = a4*q = 100*0,5 = 50
Portanto, interpolando 4 meios geométricos entre 800 e 25, obtemos a seguinte PG:
(800, 400, 200, 100, 50, 25)
a2 = a1*q = 800*0,5 = 400
a3 = a2*q = 400*0,5 = 200
a4 = a3*q = 200*0,5 = 100
a5 = a4*q = 100*0,5 = 50
Portanto, interpolando 4 meios geométricos entre 800 e 25, obtemos a seguinte PG:
(800, 400, 200, 100, 50, 25)
Vamos testar com um probleminha:
O 5º termo de uma P.G. é igual a 112 e o 1º termo é igual a 7. Determine a razão dessa P.G.
então, temos 1º,2º,3º,4º e 5º. o 1º vou chamar de a1 é = 7; o a5 é =112
"q" é o quociente.
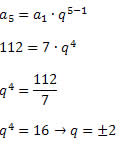
Vejam "q" elevado a 4ª potência exerce uma relação de igualdade com 16, não exerce?
qual o nº que elevado a 4ª potência resultaria 16? O nº 2 .Ou lançamos os dois lados da igualdade a raiz quarta.
Existe uma fórmula para calcular PG? Sim.
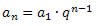
Determinando o termo geral da P.G.
Qualquer termo de uma P.G. pode ser determinado quando conhecemos o 1º termo (a1) e a razão (q). Observe o processo abaixo.
Qualquer termo de uma P.G. pode ser determinado quando conhecemos o 1º termo (a1) e a razão (q). Observe o processo abaixo.
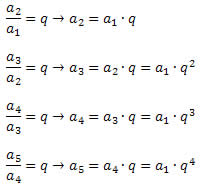
Exemplo 1. Determine o 10º termo da P.G. (3, 9, 27, ...).
Solução: temos que
a1 = 3 q = 9/3 = 3 a10 = ?
Usando a fórmula do termo geral, obtemos:
a10 = 3∙3(10-1)
a10 = 3∙39 = 59049
Solução: temos que
a1 = 3 q = 9/3 = 3 a10 = ?
Usando a fórmula do termo geral, obtemos:
a10 = 3∙3(10-1)
a10 = 3∙39 = 59049
Exemplo 2. Determine o 15º termo da P.G. (-2, 10, - 50, 250, ...).
Solução: sabemos que
a1 = - 2 q = 10/(-2) = -5 a15 = ?
Vamos utilizar a fórmula do termo geral da P.G.
a15 = -2∙(-5)(15-1) = -2∙(-5)14 = -12.207.031.250
Solução: sabemos que
a1 = - 2 q = 10/(-2) = -5 a15 = ?
Vamos utilizar a fórmula do termo geral da P.G.
a15 = -2∙(-5)(15-1) = -2∙(-5)14 = -12.207.031.250
SOMA DOS TERMOS DE UMA PG
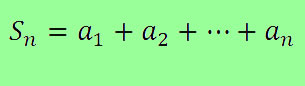
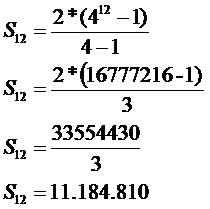
Exemplo 2
Um tipo de bactéria divide-se em duas a cada hora. Após 12 horas, qual será o número de bactérias?
a1: 1
q: 2
n: 12
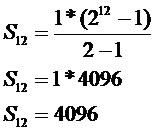
Após 12 horas o número de bactérias será igual a 4096.
Exemplo 3
Ao ser atacada por uma praga desconhecida, os frutos de uma mangueira foram apodrecendo dia após dia, obedecendo a uma progressão geométrica de primeiro termo igual a 2 e razão igual a 3. Se no décimo dia apodreceram os últimos frutos, calcule o número de frutos atacados pela praga.
Resolução:
Podemos analisar a situação da seguinte forma:
Exemplo 3
Ao ser atacada por uma praga desconhecida, os frutos de uma mangueira foram apodrecendo dia após dia, obedecendo a uma progressão geométrica de primeiro termo igual a 2 e razão igual a 3. Se no décimo dia apodreceram os últimos frutos, calcule o número de frutos atacados pela praga.
Resolução:
Podemos analisar a situação da seguinte forma:
1º dia
|
2º dia
|
3º dia
|
4º dia
|
2
|
6
|
18
|
54
|
a1: 2
q: 3
n: 10
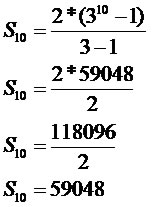
q: 3
n: 10
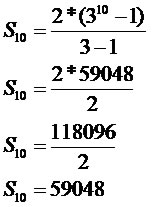
O número de frutos atacados pela praga será de 59.048.
Exemplo 4
Uma pessoa resolve guardar um dinheiro obedecendo a uma progressão geométrica de razão 2. Considerando que no primeiro mês ela irá poupar R$ 0,50, qual será o valor poupado no oitavo mês e o total guardado no período?
Valor guardado no 8º mês.
an = a1*qn–1
a8 = 0,5*28–1
a8 = 0,5*27
a8 = 0,5*128
a8 = 64
No oitavo mês ela irá poupar R$ 64,00.
Total poupado
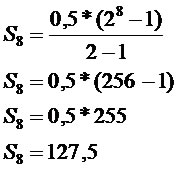
Exemplo 4
Uma pessoa resolve guardar um dinheiro obedecendo a uma progressão geométrica de razão 2. Considerando que no primeiro mês ela irá poupar R$ 0,50, qual será o valor poupado no oitavo mês e o total guardado no período?
Valor guardado no 8º mês.
an = a1*qn–1
a8 = 0,5*28–1
a8 = 0,5*27
a8 = 0,5*128
a8 = 64
No oitavo mês ela irá poupar R$ 64,00.
Total poupado
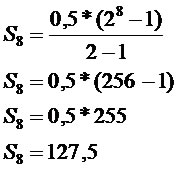
A quantia poupada no tempo determinado é de R$ 127,50.
Sabemos que a soma dos termos de uma PG finita é dada pela fórmula:
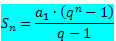
Se considerarmos uma PG com a razão sendo um número entre -1 e 1, ou seja, – 1 < q < 1, a fórmula para a soma dos termos sofre uma variação, em virtude de a razão estar compreendida nesse intervalo. Acontece que para – 1 < q < 1, à medida que o número de elementos n aumenta indefinidamente (tende ao infinito), a expressão qnse aproxima muito de zero (tende a zero). Dessa forma, ao substituir qn por zero, a fórmula da soma fica:
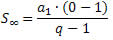
Ou
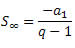
Que pode ser reescrita como:
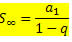
Que é a fórmula da soma dos termos de uma PG infinita com – 1 < q < 1.
Vejamos alguns exemplos de aplicação da fórmula.
Vejamos alguns exemplos de aplicação da fórmula.
Exemplo 1. Dada a PG (1,1/2,1/4,1/8,1/16…), obtenha a soma de todos os seus termos.
Solução: Temos que:
a1 = 1
Solução: Temos que:
a1 = 1
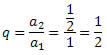
Segue que:
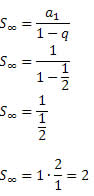
Exemplo 2. Resolva a equação:
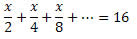
Solução: Observe que o lado esquerdo da igualdade é a soma dos infinitos termos de uma PG de razão:
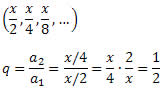
Para resolver a equação precisamos determinar qual a soma dos termos do lado esquerdo da igualdade. Para isso utilizaremos a fórmula da soma dos termos da PG infinita.
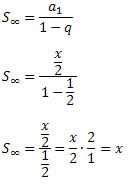
Assim, podemos reescrever o lado esquerdo da igualdade da seguinte forma:
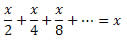
Dessa forma, teremos:
x = 16
Portanto a solução da equação é x = 16.
x = 16
Portanto a solução da equação é x = 16.
fontes:http://alunosonline.uol.com.br/matematica/progressao-geometrica.html///Por Marcelo Rigonatto///Por Marcos Noé///

Nenhum comentário:
Postar um comentário